Graph Data Structure And Algorithms

• A Graph is a non-linear data structure consisting of nodes and edges. The nodes are sometimes also referred to as vertices and the edges are lines or arcs that connect any two nodes in the graph. More formally a Graph can be defined as,A Graph consists of a finite set of vertices(or nodes) and set of Edges which connect a pair of nodes.
• In the above Graph, the set of vertices V = {0,1,2,3,4} and the set of edges E = {01, 12, 23, 34, 04, 14, 13}.
• Graphs are used to solve many real-life problems. Graphs are used to represent networks. The networks may include paths in a city or telephone network or circuit network. Graphs are also used in social networks like linkedIn, Facebook. For example, in Facebook, each person is represented with a vertex(or node). Each node is a structure and contains information like person id, name, gender, locale etc.

Continue Reading

Quick Sort in java

• This algorithm uses idea of divide and conquer.
• Find the element called pivot which divides the array into two halves
• Left side elements should be smaller than the pivot
• Right side elements are geater than the pivot
• Steps
• Bring the pivot to its appropriate position such that left of the pivot is smaller and right is greater.
• Quick sort left part
• Quick sort right part
• There are many different versions of quickSort that pick pivot in different ways.
• Always pick first element as pivot.
• Always pick last element as pivot (implemented below)
• Pick a random element as pivot.
• Pick median as pivot
• 
  
• Reference:

Continue Reading

LRU Cache Implementaion

• LRU Cache (Java) Design and implement a data structure for Least Recently Used (LRU) cache. 
• The LRU caching scheme is to remove the least recently used frame when the cache is full and a new page is referenced which is not there in cache.
• Properties are,
• Fixed Size: Cache needs to have some bounds to limit memory usages.
• Fast Access: Cache Insert and lookup operation should be fast , preferably O(1) time.
• Replacement of Entry in case , Memory Limit is reached: A cache should have efficient algorithm to evict the entry when memory is full.
• When we think about O(1) lookup , obvious data structure comes in our mind is HashMap. HashMap provide O(1) insertion and lookup.
• but HashMap does not has mechanism of tracking which entry has been queried recently and which not.To track this we require another data-structure which provide fast insertion ,deletion and updation , in case of LRU we use Doubly Linkedlist . 
• Reason for choosing doubly LinkList is O(1) deletion , updation and insertion if we have the address of Node on which this operation has to perform.
•  HashMap will hold the keys and address of the Nodes of Doubly LinkedList . And Doubly LinkedList will hold the values of keys.
• As We need to keep track of Recently used entries, We will use a clever approach. We will remove element from bottom and add element on start of LinkedList and whenever any entry is accessed , it will be moved to top. so that recently used entries will be on Top and Least used will be on Bottom.

• package com.iwq.LRU.withhashmap; import java.util.HashMap; import java.util.Map; public class LRUcache { Map hashmap = new HashMap(); Entry start; Entry end; int LRU_SIZE = 4; public void put(int key, int value) { // if key already exists update value and move to top if (hashmap.containsKey(key)) // Key Already Exist, just update the value and move it to top { Entry entry = hashmap.get(key); entry.value = value; removeNode(entry); addAtTop(entry); } else { Entry newnode = new Entry(); newnode.left = null; newnode.right = null; newnode.value = value; newnode.key = key; if (hashmap.size() > LRU_SIZE) // We have reached maxium size so need to make room for new element. { hashmap.remove(end.key); removeNode(end); addAtTop(newnode); } else { addAtTop(newnode); } hashmap.put(key, newnode); } } public void removeNode(Entry node) { // remove from left and right nodes if (node.left != null) { node.left.right = node.right; } else { start = node.right; } if (node.right != null) { node.right.left = node.left; } else { end = node.left; } } public void addAtTop(Entry node) { // node.right = start; node.left = null; if (start != null) start.left = node; start = node; if (end == null) end = start; } }

Continue Reading

Java Algorithms Trees

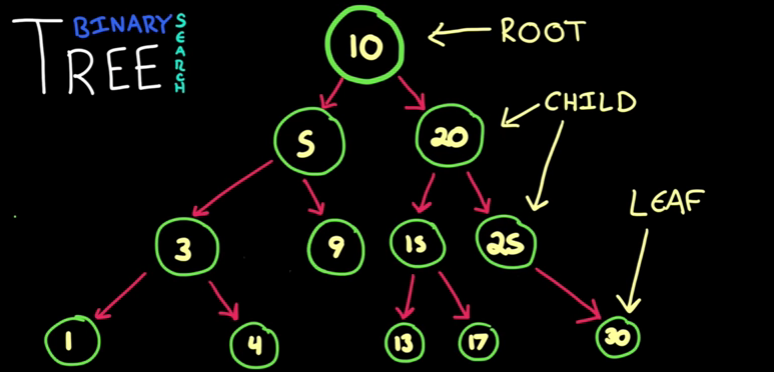
• A tree will have a root node on its top and it has child and child have child. 
• Node with out child are called leaf.
• A Binary Tree contains nodes with two children always.Each node has left node and right node. 
• Binary search tree is a binary tree having specific ordering. Here always left node contains lesser and right node contains higher values. This ordering will make finding a node very fast. 
  
• Insertion: There are two types of insertion are there Balanced and Unbalanced 
  
• Balanced Insertion
• Inserts on next free child based on left right order and time complexity will be lesser here.
• Unbalanced Insertion
•  insert go deep of list and time complexity is higher. 
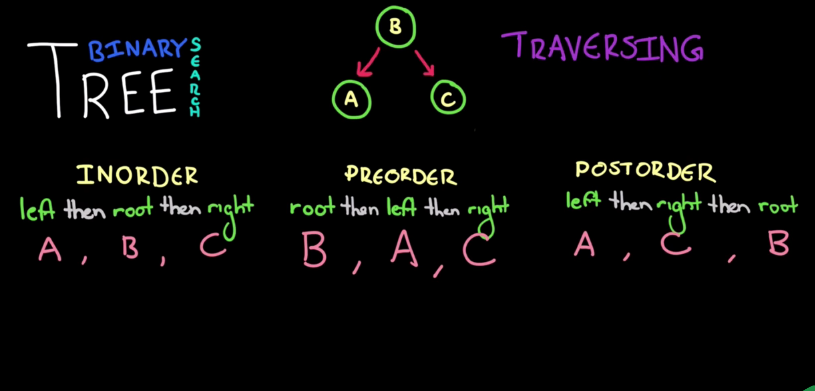
•  Traversing 
  
• In-order Traverse
  
•  Visit left node first then root node and then right node
•  Pre-order
• Visit root node first then left node and right node.
• Post-Order 
• Visit left node first then right node and last root node. 
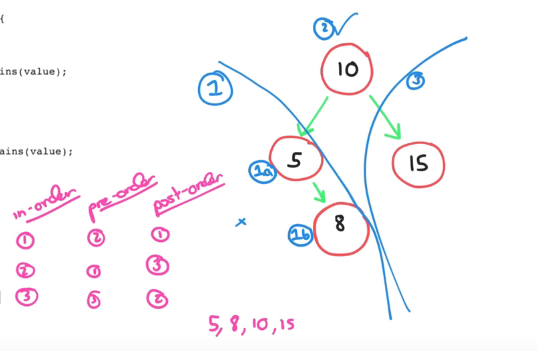
•  Code approach 
• For Insert 
• Compare value with root value.
•  If value lesser or equal to root value then go to left child node. Put value in child node if child node is null.
• If child node not null then pass the value to insert method of child. 
• If value is greater than root node value then do the same with right node. 
• For Contains 
• Check node value equals to value. 
• If equals then return true. 
• Else if value lesser than root value then go to left. If left node is null return false else call contains method of left node.
• Else if value greater than root node value then go to right node and do the same there.

public class Node { int data; Node left; Node right; public Node(int data) { this.data = data; } public void insert(int value) { if (value <= data) { // inserting if left node is free if (left == null) { left = new Node(value); } else { // forward to next node if left node aleady occupied. left.insert(value); } } else { if (right == null) { right = new Node(value); } else { right.insert(value); } } } public boolean contains(int value) { if (data == value) { return true; } else if (value < data) { if (left == null) { return false; } else { left.contains(value); } } else { if (right == null) { return false; } else { right.contains(value); } } return false; } public void inOrderPrinting() { if (left != null) { left.inOrderPrinting(); } System.out.println(data); if (right != null) { right.inOrderPrinting(); } } }

Reference Link https://www.youtube.com/watch?v=oSWTXtMglKE

Continue Reading

Java Algorithms Bubble Sort

• Bubble Sort is the simplest sorting algorithm that works by repeatedly swapping the adjacent elements if they are in wrong order. 
•  Getting each element one by one and comparing it with adjacent elements and swapping the positions.

public void bubbleSort() { int temp, firstValue, secondValue; int[] arr = { 1, 90, 25, 22, 4, 50 }; printArray(arr); for (int i = 0; i < arr.length; i++) { // #arr.length - 2 -- avoids next index of last index -- secondValue for (int j = 0; j < arr.length - 2; j++) { firstValue = arr[j]; secondValue = arr[j + 1]; if ((firstValue > secondValue)) { temp = firstValue; arr[j] = secondValue; arr[j + 1] = temp; } } } System.out.println("-----SORTING DONE-----"); printArray(arr); }

 
Reference Link https://www.youtube.com/watch?v=T8ErAYobcbc matrix

Continue Reading

Java Algorithms Linear Search

A linear search traverse down a list, one item at a time, without jumping.

public String linearSearchForValue(int value) { String indexesWithValue = ""; for (int i = 0; i < size; i++) { if (theArray[i] == value) { indexesWithValue += i + " ,"; } } return indexesWithValue; }

Continue Reading